学校

汪清县第一中学

设计者

李冰洁

课型

新授

教学内容

内容解析

（课标内容、单元内容等）

矩形的概念、矩形的性质、直角三角形斜边上的中线等于斜边的一半

矩形是特殊的平行四边形，因此矩形具有一般平行四边形的全部性质．作为一种特殊的平行四边形，矩形还具有一般平行四边形不具有的特殊性质．矩形的研究突出体现了从一般到特殊的思路．从动态的角度看，一个平行四边形在变形过程中，对边平行且相等关系不会改变，但内角的度数与对角线的长度会随之改变．特别地，当平行四边形的一个角变为直角时，其余三个角也变为直角，此时对角线不仅互相平分而且长度相等．这是一个从一般到特殊的动态演变过程，其研究思路与方法对其他特殊平行四边形的学习有借鉴作用.

“直角三角形斜边上的中线等于斜边的一半”这个结论，是由矩形对角线相等且互相平分得到的．它是研究矩形性质过程中自然发现的结论，是利用特殊平行四边形研究三角形的一个典范，体现了四边形与三角形间的联系．这个结论是直角三角形的一个重要性质，在今后学习中有着广泛的应用

基于以上分析，本节课的教学重点是：短形不同于一般平行四边形的特殊性质的发现、证明与初步应用.

教学目标

1.理解矩形的概念，明确矩形与平行四边形的区别和联系，体会特殊与一般之间的关系．

2.探究矩形的性质和识别条件，提高学生的推理能力．

3.利用矩形的性质定理进行证明和计算．

4.掌握直角三角形斜边上的中线的性质，会用它解决求线段长或线段倍分关系的问题.

目标解析

目标（1） 的具体要求是：理解矩形的概念，要求学生明确矩形是特殊的平行四边形，知道矩形的定义是探究矩形性质和判定的出发点．

目标（2）的具体要求是：经历对矩形性质的理性思辨和整理归纳的过程，形成对矩形性质的完整认识，明确性质的条件与结论，能在不同情境和复杂问题中，综合运用矩形的性质解决相关问题.

目标（3）的具体要求是：理解“直角三角形斜边上的中线等于斜边一半” 这一重要结论，会应用这一结论解决简单的问题.

教学重点

矩形性质定理和直角三角形斜边上的中线的性质的理解与运用

教学难点

矩形性质定理和直角三角形斜边上的中线的性质的探究与证明

教学方法

讲授法。小组讨论法

教

学

过

程

设

计

教学内容及教师活动

【情境导入】

拿一个活动的平行四边形教具，轻轻拉动一个点，它还是平行四边形吗？使一个角是直角，这时它是什么图形？(动画演示拉动过程如图)

概念引入：有一个角是直角的平行四边形叫做矩形，也就是长方形．

仔细观察下列实际生活中的图片，你觉得哪些是矩形的形象？

矩形是生活中很常见的图形，你还能列举出矩形在生活中应用的其他例子吗？我们一起来探讨一下矩形的性质吧！

探究点1　矩形的性质

如图，取一张矩形纸片，用直尺画出它的对角线．

1.矩形是特殊的平行四边形，它和平行四边形相比，

有什么特殊之处？答：有一个角是直角．

2．平行四边形的对角相等，邻角互补，那么矩形的四个角会有怎样的关系呢？答：矩形的四个角都相等，都是直角．

3．测量我们刚刚折纸时的两条对角线长度，这两个长度有什么关系？

答：两条对角线长度相等．

下面我们一起来验证一下：

1.如图，在矩形ABCD中，∠A＝90°.求证：∠A＝∠B＝∠C＝∠D＝90°.

2.如图，四边形ABCD是矩形．求证：AC＝BD.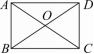

归纳总结：矩形的四个角都是直角；矩形的对角线相等．

【对应训练】

1．矩形具有而一般平行四边形不具有的性质是( D )

A．对边平行　　　B．对边相等　　　C．对角相等　D．对角线相等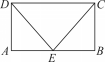

2．如图，在矩形ABCD中，E是AB的中点，连接DE，CE.求证：△ADE≌△BCE.

3．教材P53练习第3题．

探究点2　直角三角形斜边上的中线的性质

如图，矩形ABCD的对角线AC，BD相交于点O.我们观Rt△ABC，在Rt△ABC中，BO是斜边AC上的中线，BO与AC有什么关系？

1．矩形ABCD的对角线AC把矩形分成了两个三角形，在△ABC中∠ABC是什么角？

答：直角．

2．AO与CO有什么关系？BO与DO有什么关系？

答：AO＝CO，BO＝DO.

3．BO与BD有什么关系？与AC又有什么关系？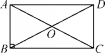

答：BO＝BD，BO＝AC.

归纳总结：直角三角形斜边上的中线等于斜边的一半．

例1　(教材P53例1)如图，矩形ABCD的对角线

AC，BD相交于点O，∠AOB＝60°，AB＝4，

求矩形对角线的长．

分析：因为矩形是特殊的平行四边形，所以它具有对角线相等且互相平分的性质．根据矩形的这个性质和已知条件，可得△OAB是等边三角形，因此可求对角线的长度．

【对应训练】

1.如图，在△ABC中，∠ACB＝90°，AD＝BD，

CD＝4，则AB的长为( A )

A．8　　　　　　B．6　　　C．4　　　　D．2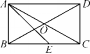

2．如图，O是矩形ABCD对角线的交点，∠AOD＝120°，AE平分∠BAD，则∠EAC＝15°.

3．教材P53练习第2题．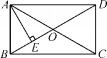

例2　如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，且BE∶ED＝1∶3，AD＝6 cm.求AE的长．

【对应训练】

1．如图，在矩形ABCD中，对角线AC，BD相交于点O，点E，F分别是AO，AD的中点，连接EF.若AB＝6 cm，BC＝8 cm，则EF的长是( D )

A．2.2 cm　　　B．2.3 cm

C．2.4 cmD．2.5 cm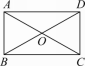

2．如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB＝5，AD＝12，求四边形ABOM的周长．

【随堂训练】见《创优作业》“随堂小练”册子相应课时训练．

【课堂总结】师生一起回顾本节课所学主要内容，并请学生回答以下问题：矩形作为特殊的平行四边形，它的概念是什么？矩形有哪些特殊的性质？直角三角形斜边上的中线的性质是什么？

【知识结构】

【作业布置】

1．教材P50习题18.1第5，11题，教材P62习题18.2第16题．

2．课时练．

学生活动

学生根据生活经验及图片思考矩形的概念，教师总结矩形的概念.

告诉学生：矩形作为特殊的平行四边形，除了具有平行四边形的所有性质外，还有一些特殊性质．注意结合教材P53练习第3题让学生熟悉矩形的对称性.

提醒学生：矩形的两条对角线将矩形分成两对全等的等腰三角形，在解题时常用到等腰三角形的性质.

设计意图

动态演示平行四边形变成矩形的过程，使学生了解矩形的概念.

通过动手操作，让学生在活动中得出矩形的性质，印象更加深刻.

引导学生发现直角三角形斜边上的中线的性质.

巩固学生对矩形性质的认知，同时要注意直角三角形斜边上的中线的性质

教学板书

18.2.1　矩形

第1课时　矩形的性质

一、矩形的概念．

二、矩形的性质：1.边；2.角；3.对角线．

三、直角三角形斜边上的中线的性质．

教学反思

本节课的主要教学任务是矩形的性质及其推论，教学中让学生充分经历从实际生活中抽象数学图形到深入认识图形特征的过程，更好地理解平行四边形与矩形之间的从属关系和内在联系，在适度的方法训练中加强知识的灵活运用，使学生对于常见的转化方法也能灵活应用.